Research Overview
In this paper, we present a comprehensive description of thermodynamics in a differential geometric setting for a general non-relativistic continuum mechanical system. In order to deal with manifestly coordinate-invariant equations valid on general Riemannian manifolds, we make use of a formulation based on exterior calculus. We show how to complement this covariant formulation, already well known in continuum mechanics, with a consistent description of thermodynamics valid in general mechanical field theories, generalizing the procedure carried through on Euclidean spaces using vector calculus.
We specialize the equations to Fourier–Navier–Stokes fluids in order to shed light on the entropy creation mechanisms in Newtonian fluids on manifolds.
1st Law of Thermodynamics (Total energy balance)
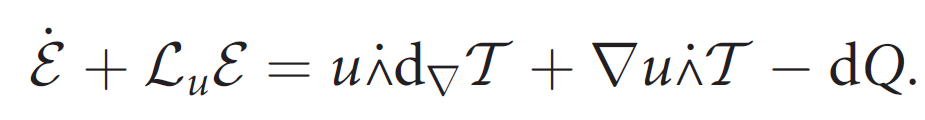
Kinetic Energy and Internal Energy balances

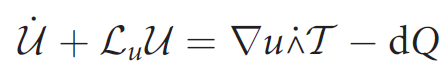
2nd Law of Thermodynamics
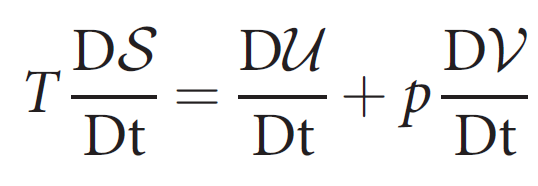
Publication
| F. Califano, R. Rashad, S. Stramigioli (2022) A differential geometric description of thermodynamics in continuum mechanics with application to Fourier-Navier-Stokes fluids, Physics of Fluids 34(10), AIP Publishing LLC, doi:10.1063/5.0119517 |
