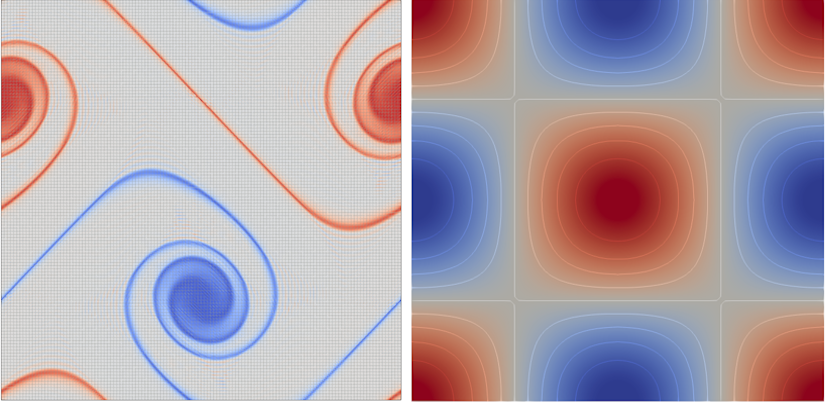
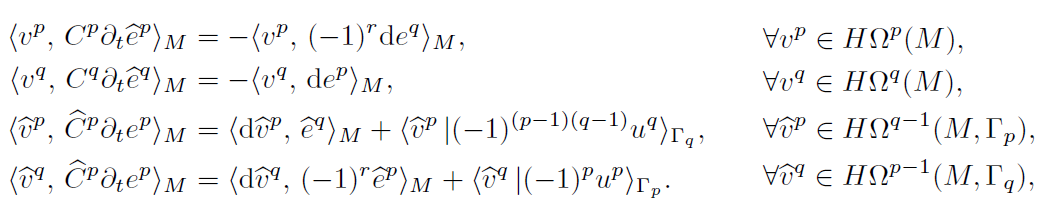Research Overview In this ongoing research, we work on the structure-preserving discretization of the incompressible Navier-Stokes (NS) equations [math] \partial_t v + \omega\times v + \frac{1}{\text{Re}} \text{curl}(\omega)+ \text{grad}(p) […]
Computational Physics
Posted on:
pHyem library
phyem is an open-source finite element library that bridges port-based thinking to numerics and enables LEGO-like simulations. The name, pHyem, stands for Python + Port-Hamiltonian + FEM + Physics. The project’s […]
Computational Physics
Posted on:
Dual-field Finite Element Exterior Calculus
Research Overview In this work we propose a novel approach to discretize linear port-Hamiltonian systems while preserving the underlying structure. We present a finite element exterior calculus formulation […]
Computational Physics
Posted on:
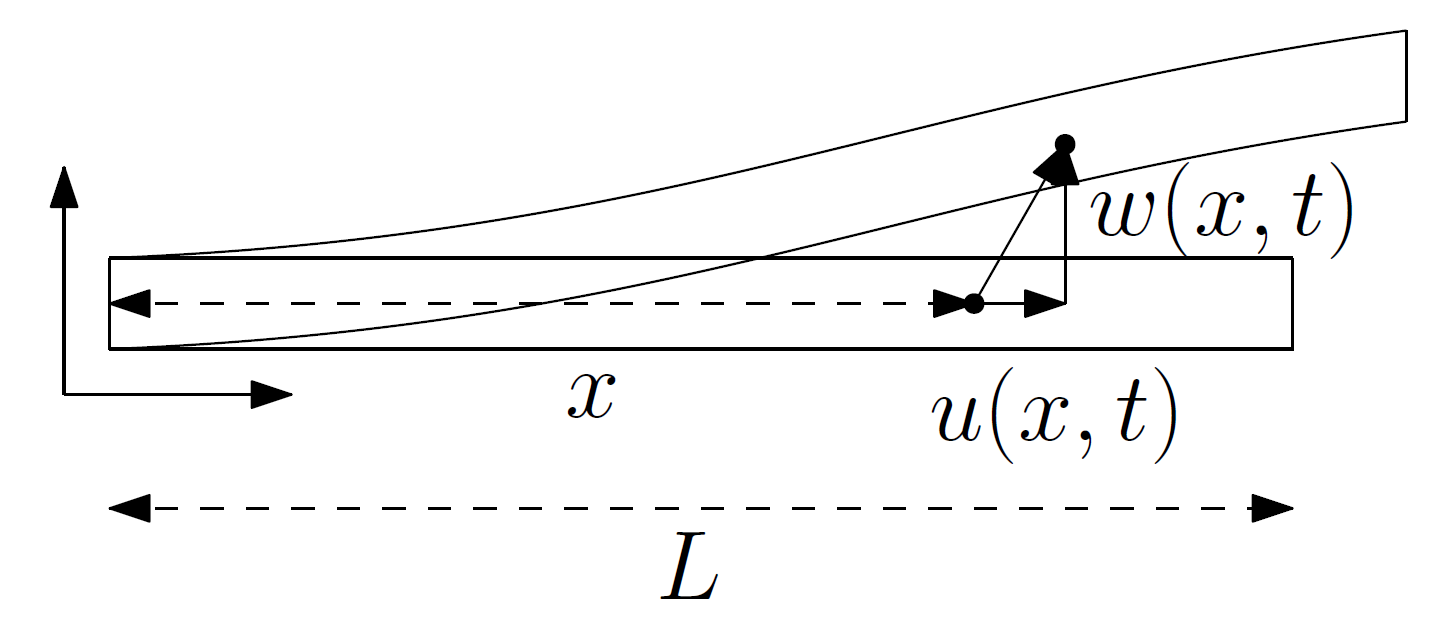
FEM of von Karman Beams
Research Overview In this contribution, the von Karman beam model is formulated as a port-Hamiltonian system. The selection of energy variables will be such to make the Hamiltonian […]