Research Overview
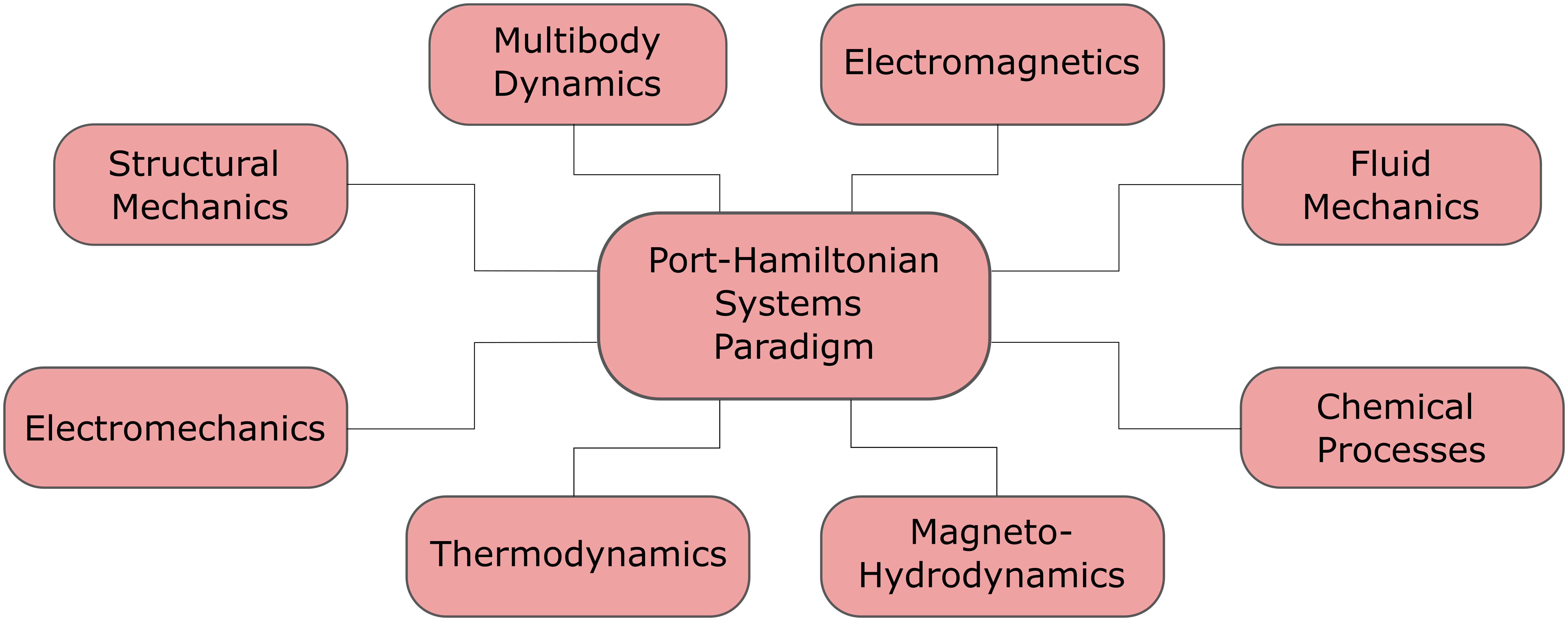
The port-Hamiltonian (pH) systems paradigm is a framework for the modeling, analysis, design, and control of complex dynamical systems. The mentioned complexity arises due to multi-physical domains, inter-domain couplings, nonlinearities, and distributed sensing and actuation. The framework’s key features include the emphasis on power flow between subsystems, the separation of the interconnection structure of the system from its components’ constitutive relations, and the exploitation of this separation in the analysis and control of the system.
The pH system theory is applicable for both lumped parameter (finite-dimensional) systems and distributed parameter (infinite-dimensional) systems.
For the past two decades, the distributed port-Hamiltonian (dpH) systems theory underwent a huge evolution that branched in different directions and is still an active area of research. The first research direction in the literature was in implementing the generic dpH theory for modeling distributed parameter systems in different physical domains. The second direction was the analysis and design of control techniques suitable for pH models by extending the well-established techniques for finite-dimensional pH systems, like energy shaping and damping injection. Another research direction was focused on generating finite dimensional approximations of the dpH models or the infinite-dimensional controllers by structure-preserving discretization methods. Finally, there has been also a lot of research efforts in different theoretical formulations of pH systems and extensions to the original framework.
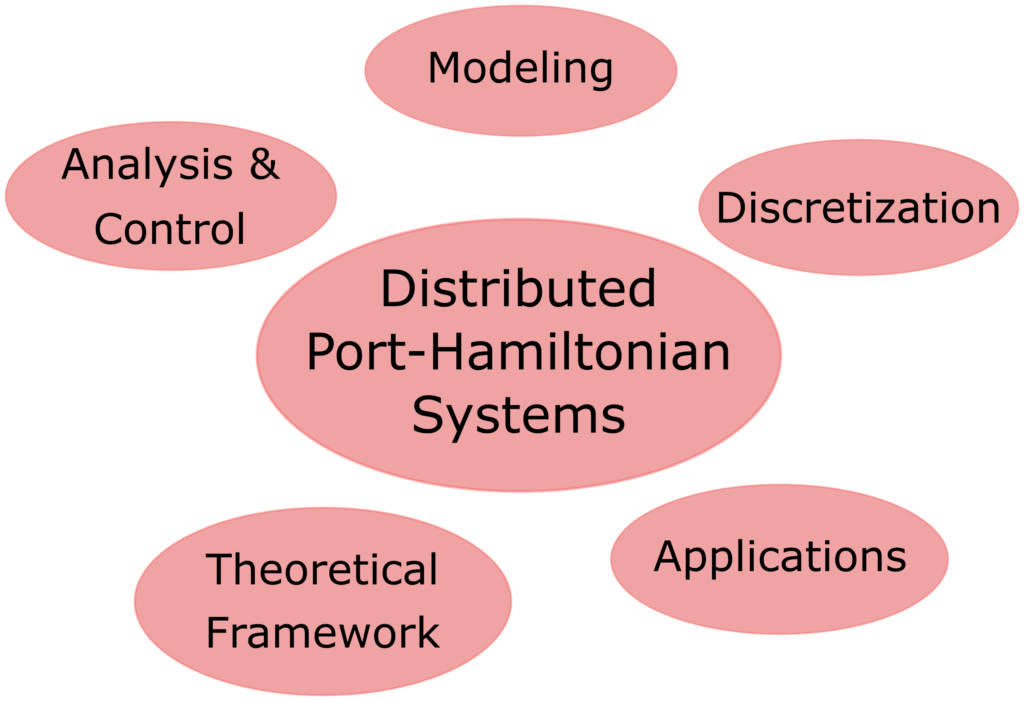
In this article we present a review of the research studies carried out in the past twenty years (approximately) relying on the work of [van der Schaft and Maschke 2002]. We classify over a hundred and forty studies into different classes depending on their respective research focus, shown in the Fig. below. The research directions considered include modeling, analysis and control, discretization, theoretical framework, and applications. The last class includes papers that combined other different techniques.
References
van der Schaft, A. J., & Maschke, B. M. (2002). Hamiltonian formulation of distributed-parameter systems with boundary energy flow. Journal of Geometry and physics, 42(1-2), 166-194.