Navier-Stokes Equations

Research Overview

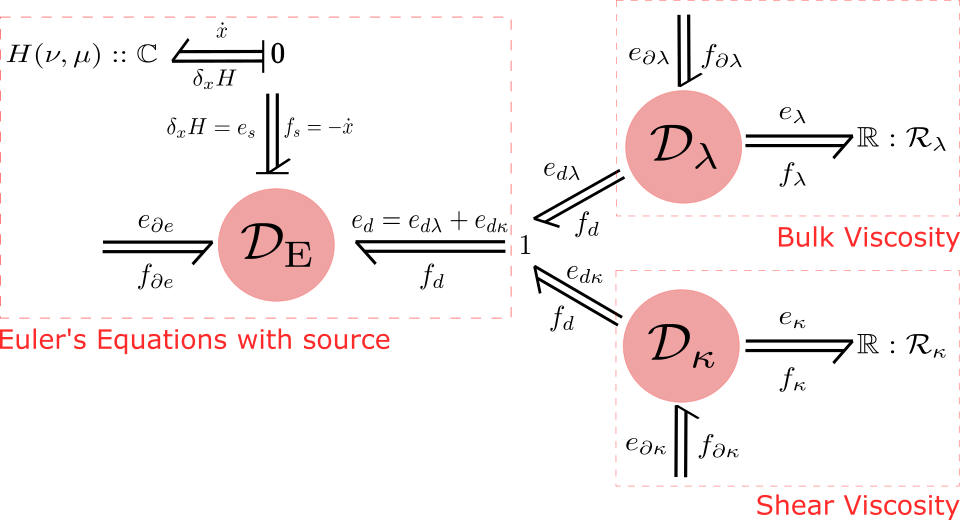
The specific aim of this work is to extend the port-Hamiltonian formulation of ideal compressible fluids (Euler equations) to Newtonian viscous fluids (Navier–Stokes equations). The way this extension is developed is consistent with the core methodology of port-Hamiltonian modeling: we introduce a distributed port to interconnect the system representing ideal fluid dynamics with a purely dissipative systemthat encodes the constitutive relations peculiar of Newtonian fluids.

The way to achieve the complete level of generality in this work is by extending the differential form representation of port-Hamiltonian fluid systems to tensor-valued forms and the identification of novel duality pairings that are necessary to extend the definition of power flows in this context.

Publications