FEM of von Karman Beams

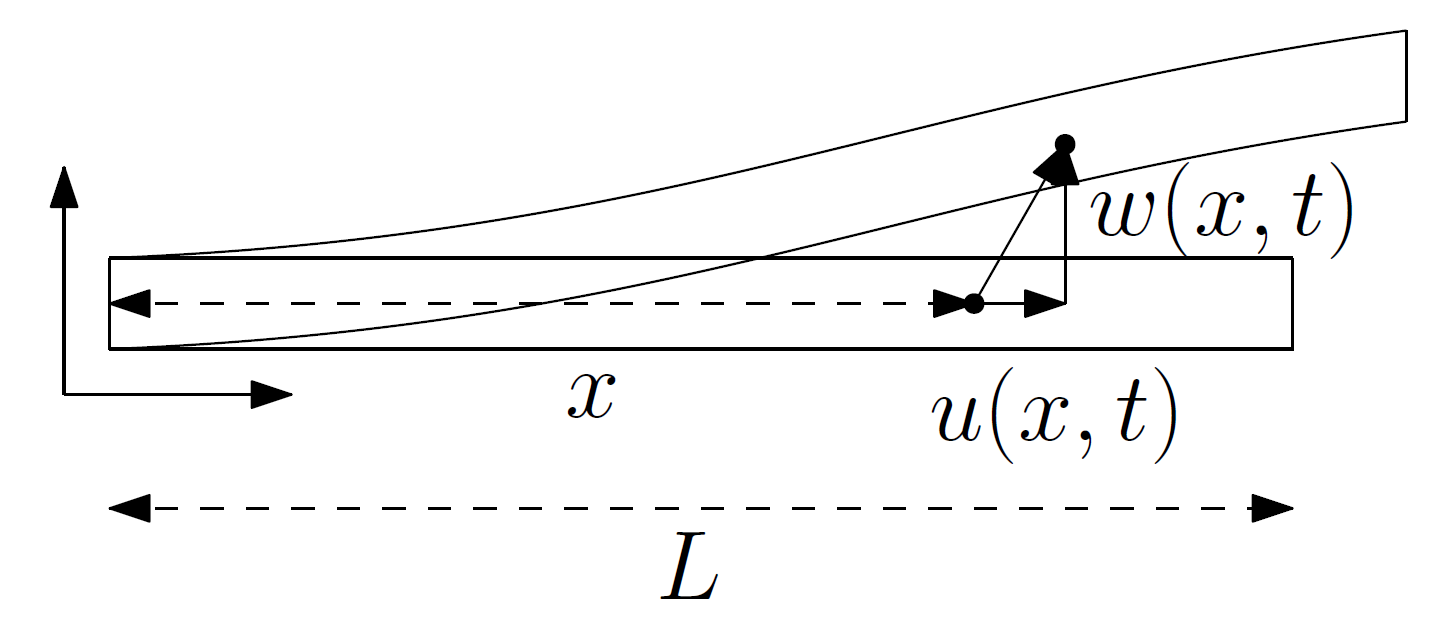
Research Overview

In this contribution, the von Karman beam model is formulated as a port-Hamiltonian system. The selection of energy variables will be such to make the Hamiltonian quadratic in these variables. As a consequence of this choice, the non linearities of the model are included in the interconnection operator, whereas the constitutive relations remain linear.
The obtained model can be discretized using mixed finite elements. To this aim, a weak formulation that does not demand for H2 regularity for the vertical displacement (as in classical Galerkin discretization of beams and plates) is obtained. This means that the vertical displacement can be discretized using H1 conforming elements (i.e. Continuous Galerkin elements),
rather then using the more computationally demanding H2 conforming elements, like the Hermite polynomials. A numerical test is carried out to evaluate the convergence rate of the discrete solution with respect to an analytical one.

The port-Hamiltonian system representing the von Karman beam model is given by

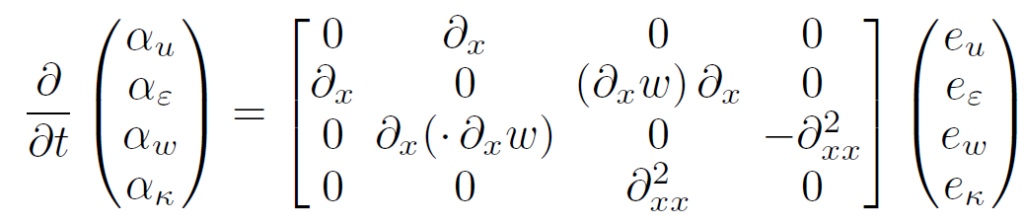
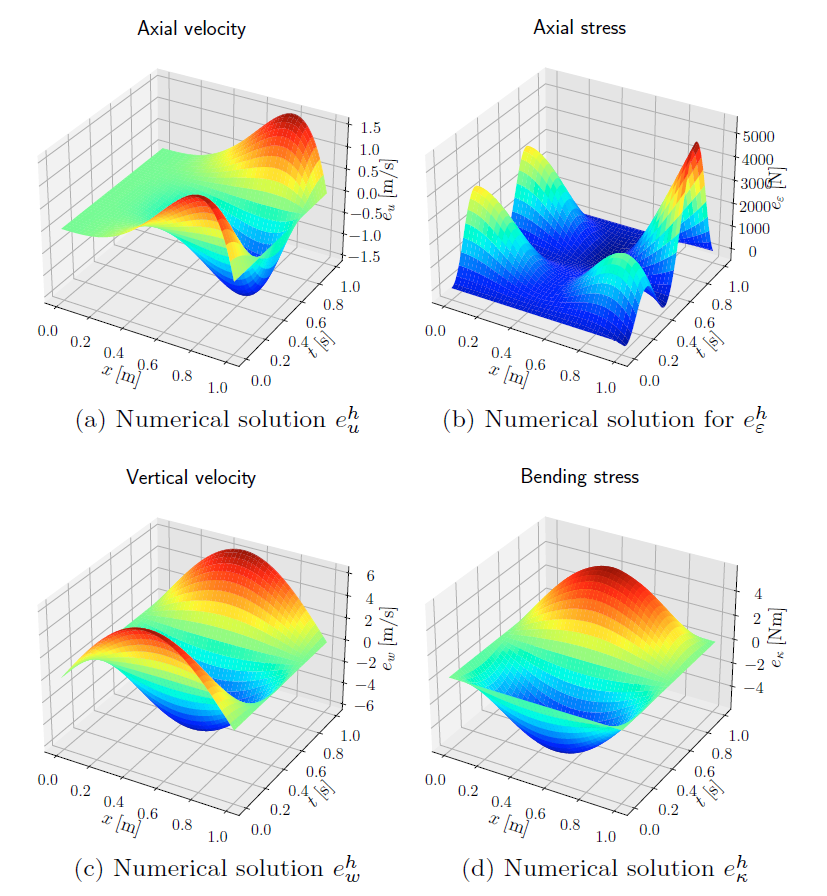
The numerical solution computed is shown below

Publication