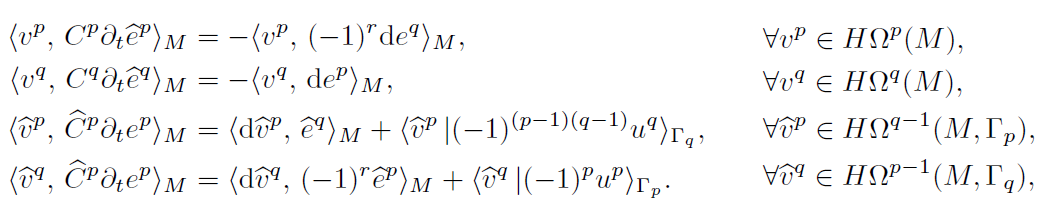Research Overview
In this work we propose a novel approach to discretize linear port-Hamiltonian systems while preserving the underlying structure. We present a finite element exterior calculus formulation that is able to mimetically represent conservation laws and cope with mixed open boundary conditions using a single computational mesh. The possibility of including open boundary conditions allows for modular composition of complex multi-physical systems whereas the exterior calculus formulation provides a coordinate-free treatment. Our approach relies on a dual-field representation of the physical system that is redundant at the continuous level but eliminates the need of mimicking the Hodge star operator at the discrete level. By considering the Stokes-Dirac structure representing the system together with its adjoint, which embeds the metric information directly in the codifferential, the need for an explicit discrete Hodge star is avoided altogether. By imposing the boundary conditions in a strong manner, the power balance characterizing the Stokes-Dirac structure is then retrieved at the discrete level via symplectic Runge-Kutta integrators based on Gauss-Legendre collocation points.
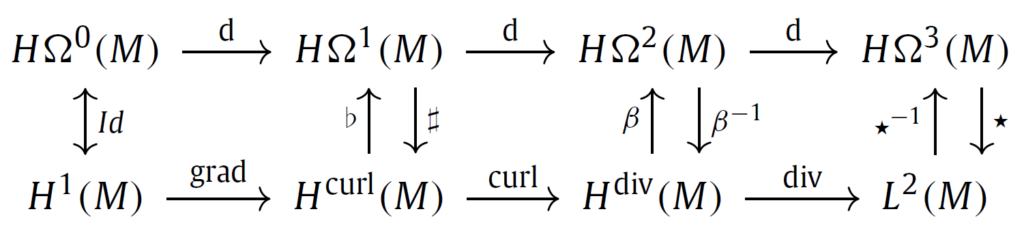
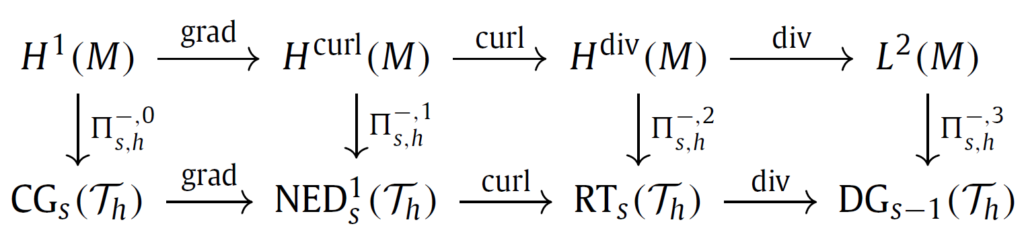


Publication
| Andrea Brugnoli, Ramy Rashad, Stefano Stramigioli (2022) Dual field structure-preserving discretization of port-Hamiltonian systems using finite element exterior calculus, Journal of Computational Physics 471, p. 111601, Elsevier Inc., doi:10.1016/j.jcp.2022.111601 |