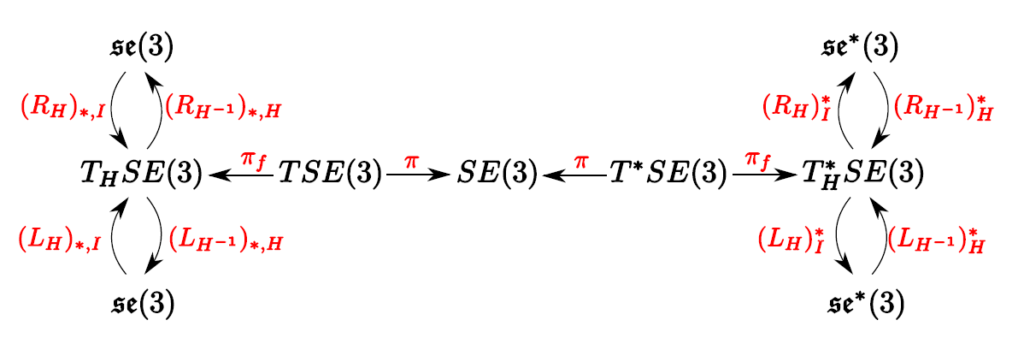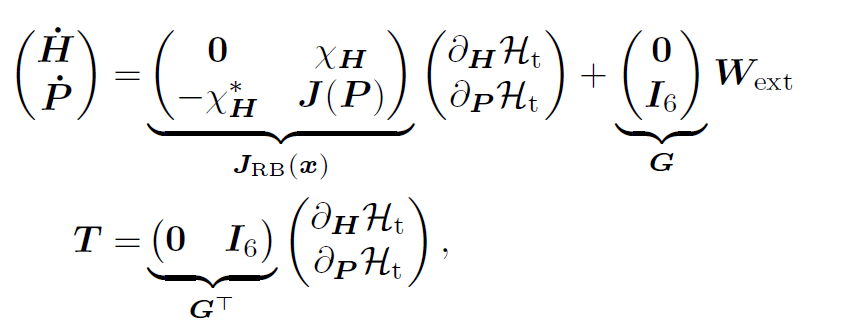by: RamyPosted on:

Rigid Body Dynamics

This work has been published as Ch.4 of my PhD thesis.

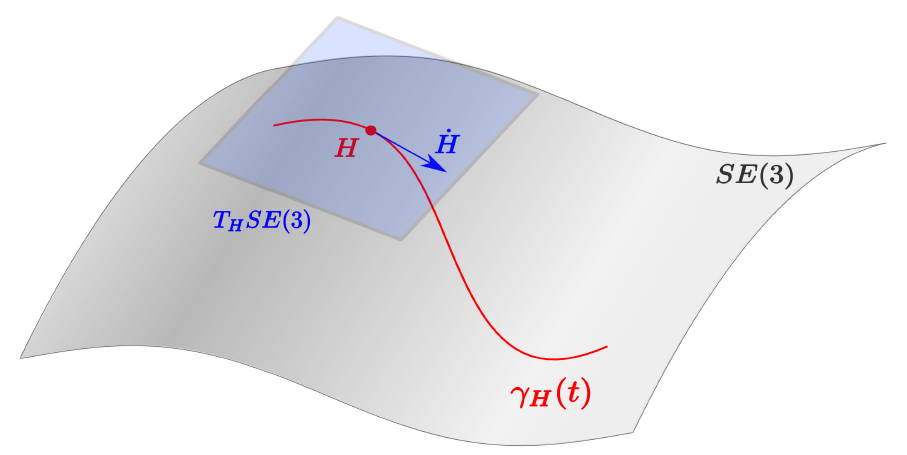
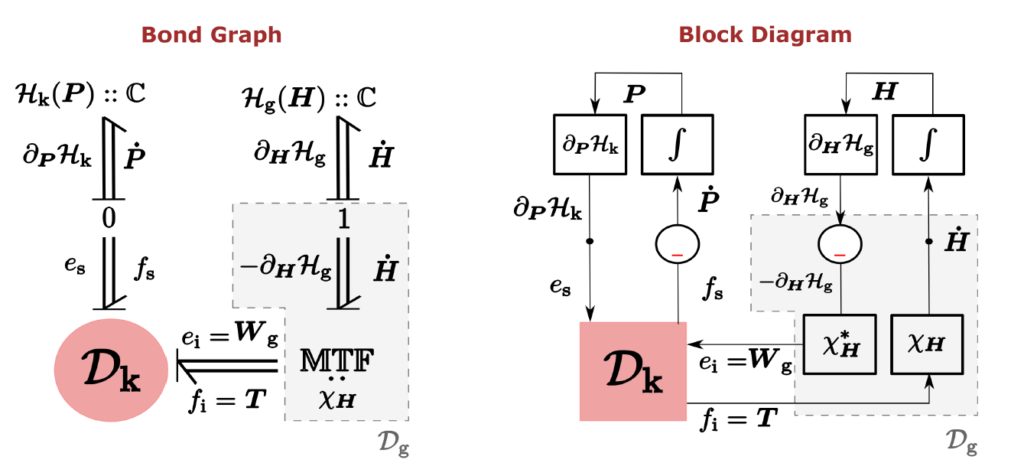
The study of rigid body modeling is central to the mathematical theories of robotics. The topic of rigid bodies is a recurrent theme for serial and parallel rigid manipulators as well as for ground, underwater, and aerial mobile robots. In this work, we consider the problem of modeling rigid body motion in the port-Hamiltonian framework using the Lie group approach for describing rigid body kinematics.

Illustration of general rigid body motion as a curve on SE(3) which represents a family of homogeneous transformation matrices
Commutative Diagram relating the Lie group SE(3) to the Lie algebra se(3) and its dual space se*(3).
Decomposed port-Hamiltonian model describing rigid body dynamics as an interconnection of energetic modules characterizing storage of kinetic and gravitational potential energy
Explicit port-Hamiltonian dynamics of a rigid body