Multirotor UAVs

Research Overview

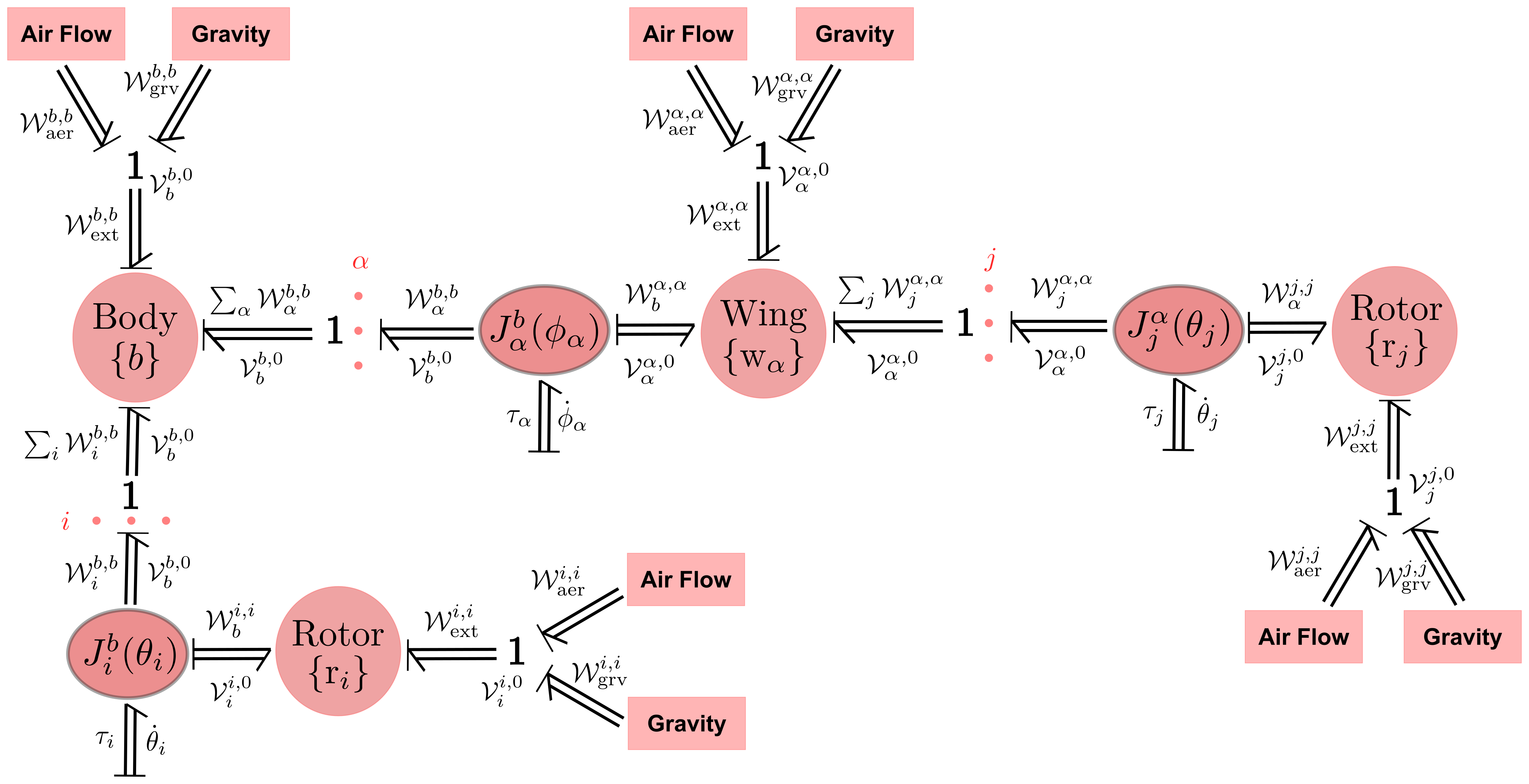
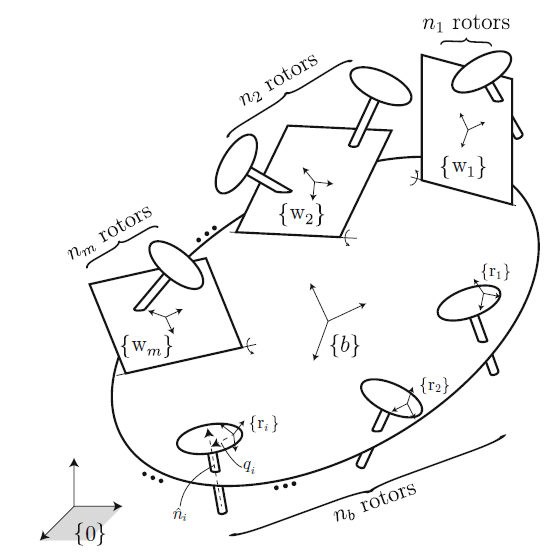
In this paper we present a systematic modeling framework for generic MAVs that encompasses a wide spectrum of possible designs. We assume the MAVs are driven by a set of rotors, possibly with tiltable axes, and that an arbitrary number of fixed and adjustable wings may be attached to the vehicle body. A subset of the rotors may be attached to the wings and some to the main MAV body. Our modeling framework considers the rigid multibody dynamics of both the vehicle body’s mass and inertia as well as the masses and inertias of the rotor bodies. In addition to the thrust forces and moments generated by the rotors, our framework allows for the consideration of external aerodynamic forces that are applied to the MAV.

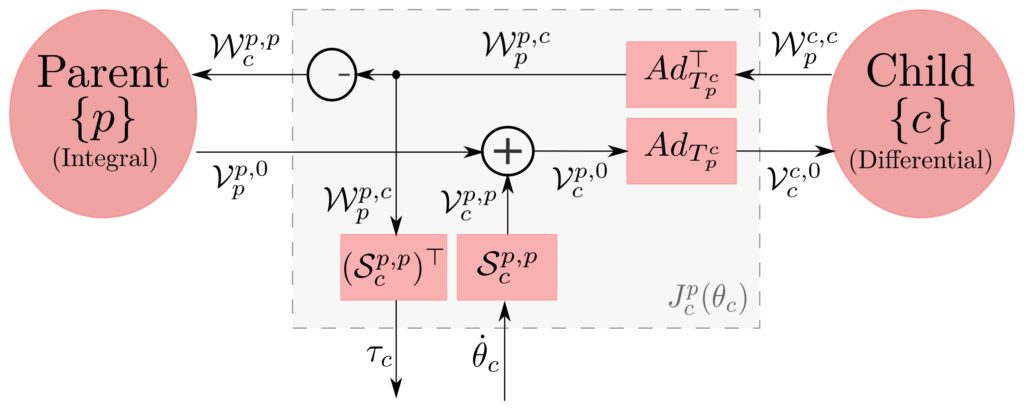
One of the distinguishing features of our approach is the adoption of modern screw-theoretic methods for multibody dynamic modeling, or more precisely, using notation and operations associated with the Lie group of rigid body motions, also commonly known as the Special Euclidean group SE(3). The use of such methods is by now quite standard in the robot dynamics literature, as the algorithms are expressed in a way that is invariant with respect to the placement of reference frames on the bodies, and closed-form expressions for derivatives of the dynamics are available for optimization and sensitivity analysis, among other applications. Here we apply the same concepts and transformations to MAV dynamic modeling and derive a reference frame-invariant set of dynamic equations for generic winged and wingless MAV models. The dynamics of MAVs with articulated structures such as a multi-dof robot arm attached to the body can also be systematically included within this framework.

By adopting the Lie group framework and the ensuing rules for the transformation of six-dimensional velocities, forces and inertias, the dynamics of complex MAVs can be derived in a straightforward and systematic way, without regard to the way in which reference frames are attached to the MAV. Moreover, the resulting equations are shown to be easily factored with respect to any of the model parameters, e.g., inertias of the body and rotors, rotor axes, aerodynamic constants and also easily differentiated. These features make our geometric formulation particularly attractive for applications such as design, calibration and identification, and also dynamics-based trajectory optimization where analytic gradients involving the dynamics are required.

Publication