Fluid-Structure-Interaction

Research Overview

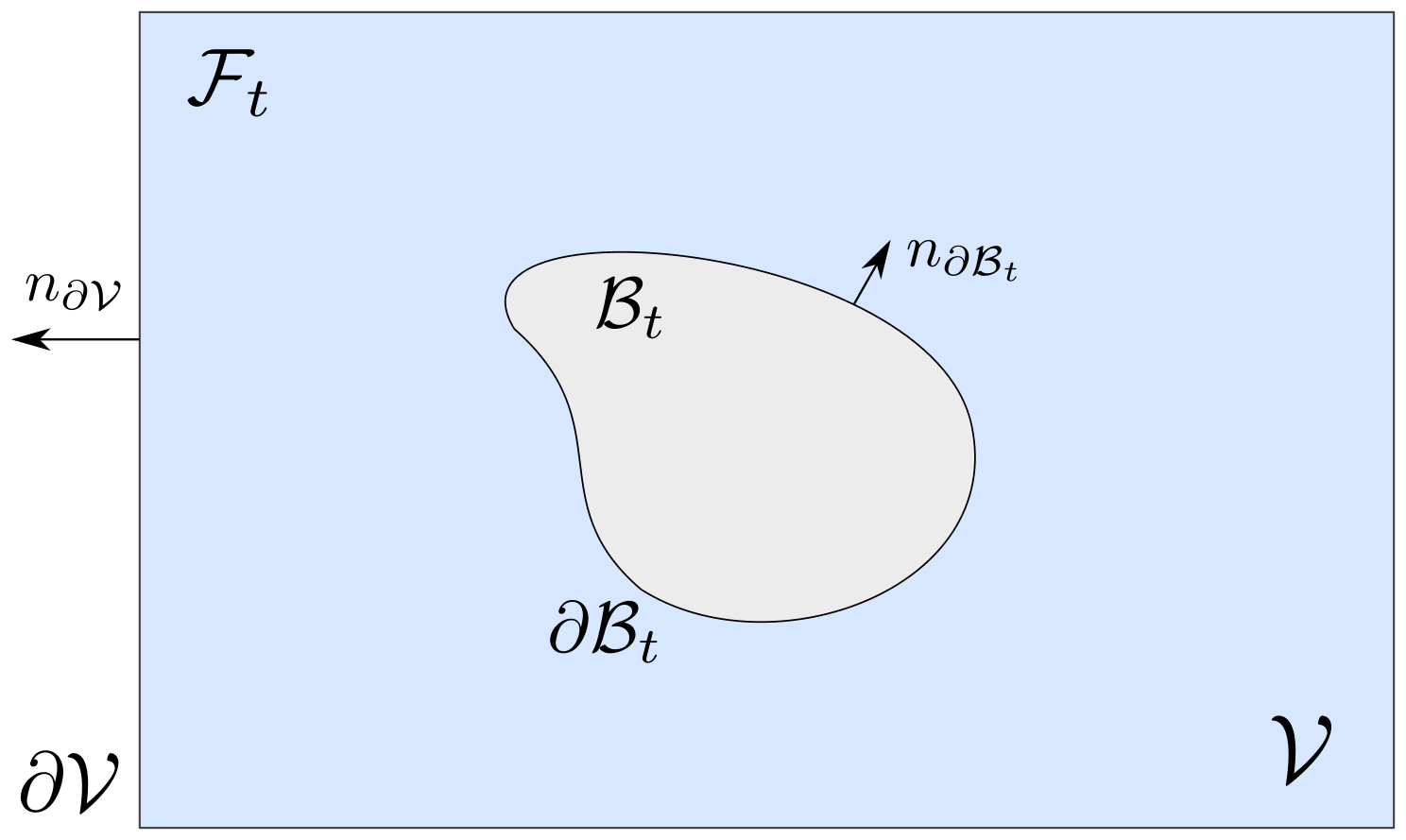
The goal of this work is to extend the existing port-Hamiltonian theory of open distributed parameter systems on fixed spatial domains to the practically relevant case where the spatial domains can vary in time. One intended application pushing this extension of the theory is a complete port-Hamiltonian study of fluid-solid interactions.

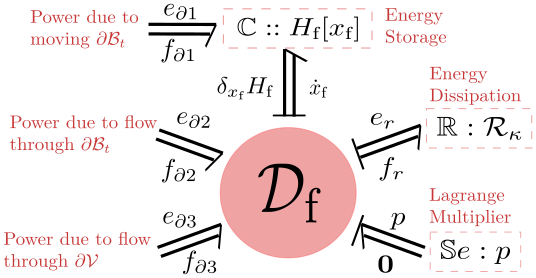
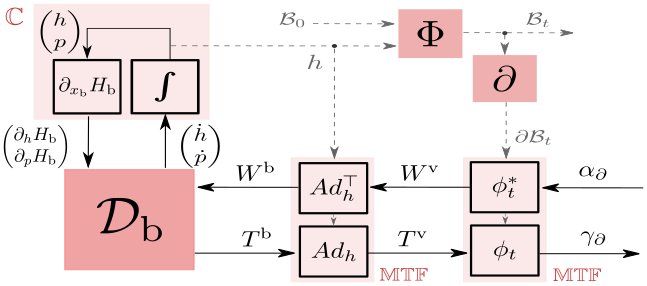
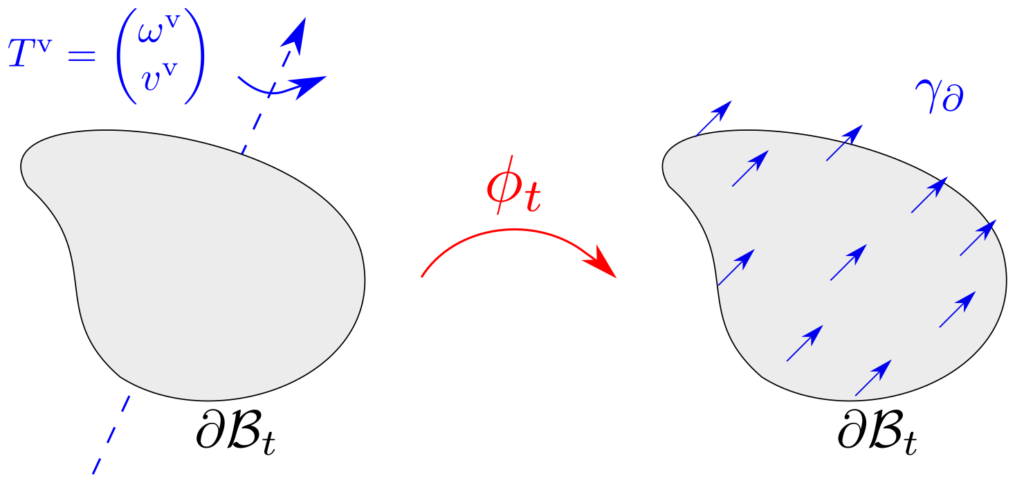
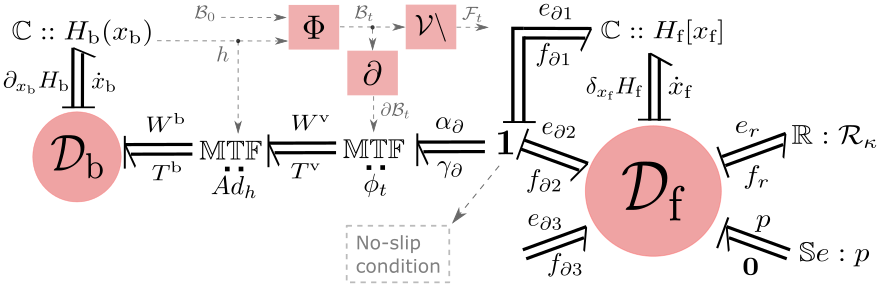
As a signature application of our techniques to treat moving domain boundaries, we study the boundary interconnection of a rigid body with a viscous fluid and provide a complete energetic decomposition of this system in port-Hamiltonian fashion. In particular, we show how the novel port-based representation of the motion of the spatial domains is necessary to correctly implement a no-slipcondition between the fluid and the solid.

One significant advantage of this decomposition of the system — into separate open subsystems and the precise structure of their interconnection via a Dirac structure — is its modularity: When needed, the overall port-Hamiltonian model can be updated by replacement, addition or removal of subsystems in order to provide either more specialised or arbitrarily more sophisticated models than the one considered here. Another advantage is that the complete port-Hamiltonian decomposition allows to analyse the power flow between all system components in order to derive conclusions on the stability of a sophisticated multi-component system or to devise novel numerical algorithms that exploit the associated conservation laws subsystem by subsystem.

Publication