Research Overview
Identifying the underlying structure of partial differential equations is a fundamental topic in modern treatments of continuum mechanics and field theories in general. Not only does every discovery of a new structure provide a better mathematical understanding of the theory, but such hidden structures are fundamental for analysis, discretization, model order reduction and controller design. Throughout the years, many efforts were made to search for the geometric, topological and energetic structures underlying the governing equations of continuum mechanics and we aim in this paper to contribute to this search.
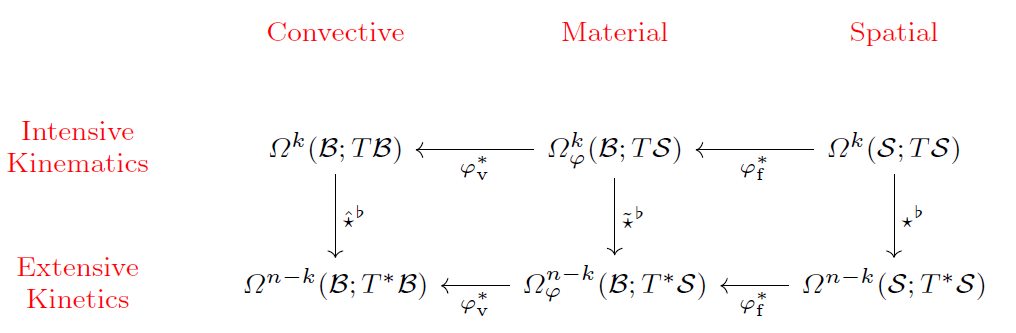
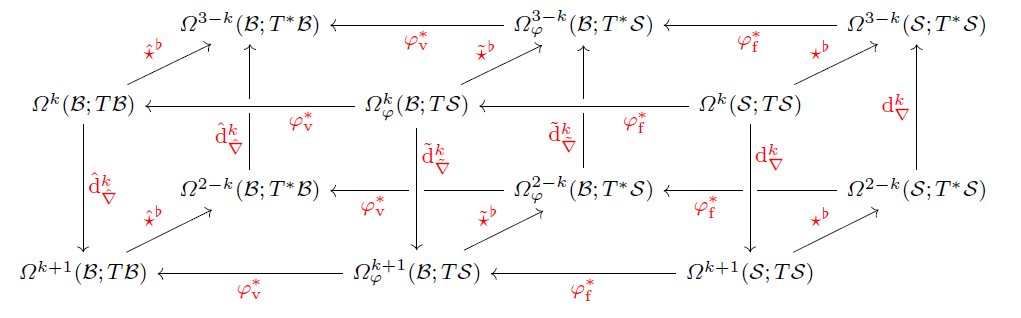
In this paper, we focus on the formulation of nonlinear elasticity using exterior calculus in a geometrically intrinsic manner. Throughout the paper, we aim to highlight the underlying geometric and topological structures of nonlinear elasticity while treating the spatial, material and convective representations of the theory.
Our formulation of nonlinear elasticity is distinguished by its minimalistic nature which simplifies the theory to its essential intrinsic coordinate-free parts. By identifying kinematic quantities (e.g. velocities and rate-of-strain variables) with appropriate intensive vector-valued forms, the momentum and stress variables will be naturally represented as extensive covector-valued pseudo-forms, by topological duality. Furthermore, using Riesz representation theorem, we will construct appropriate Hodge star operators that will relate the different variables to each other. Not only does our intrinsic formulation reflect the geometric nature of the physical variables, but also the resulting expressions of the dynamics are compact, in line with physical intuition, and one has a clear recipe for changing between the different representations. Finally, in order to target a wider audience than researchers proficient in geometric mechanics, we present the paper in a pedagogical style using several visualizations of the theory and include coordinate-based expressions of the abstract geometric objects.
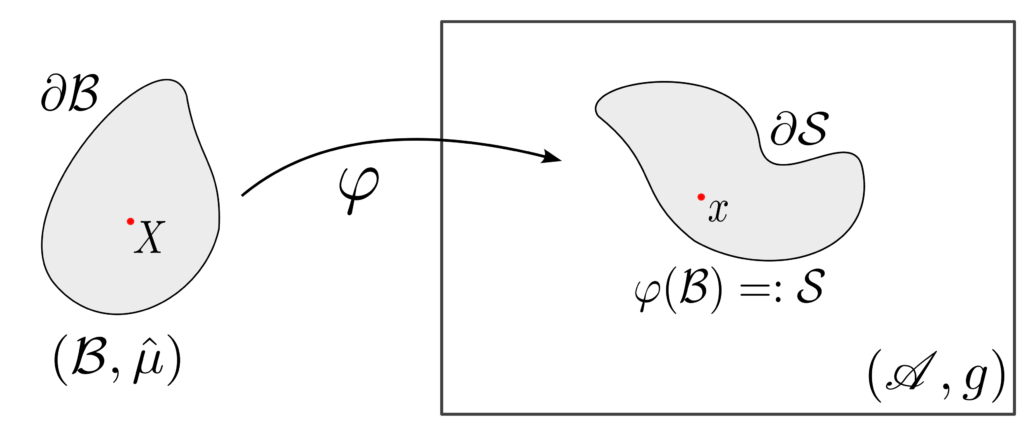
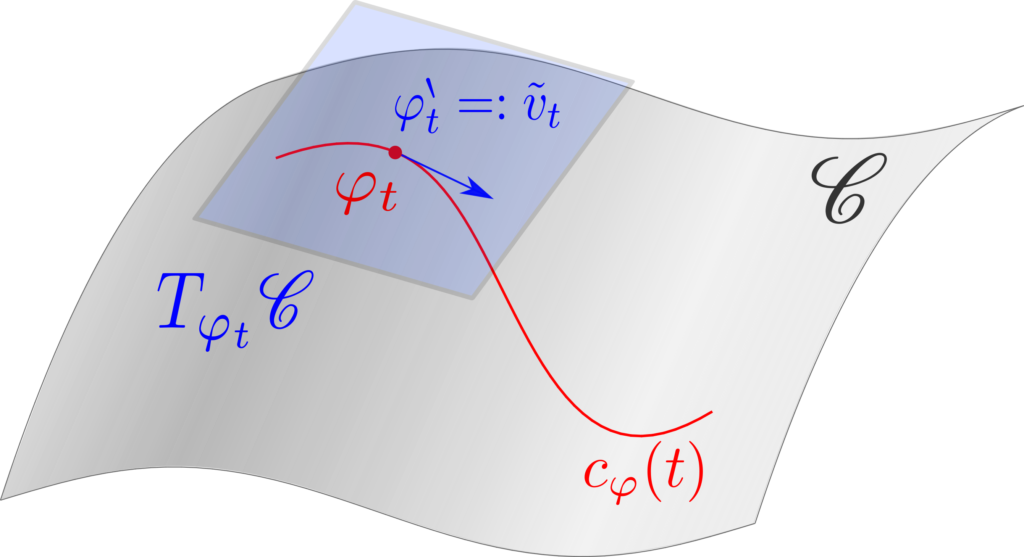
We also consider in our work emphasizing two types of structures underlying the theory of nonlinear elasticity, namely 1) the principal bundle structure relating the configuration space to the deformation space and 2) the de Rham complex structure relating the spaces of bundle-valued forms to each other.

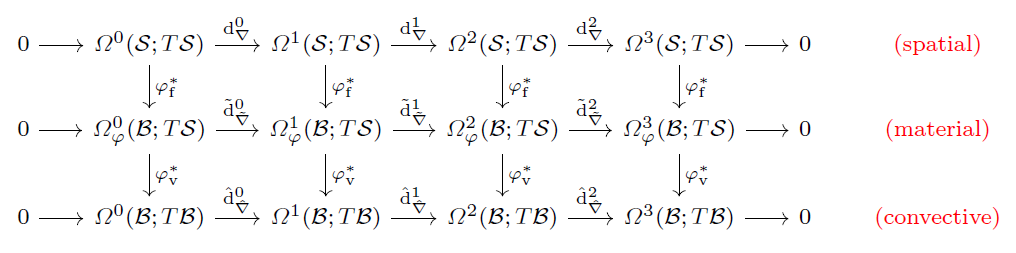
Publication
| Ramy Rashad, Andrea Brugnoli, Federico Califano, Erwin Luesink, Stefano Stramigioli (2023) Intrinsic Nonlinear Elasticity: An Exterior Calculus Formulation, Journal of Nonlinear Science 33(5), p. 84, doi:10.1007/s00332-023-09945-7 |