Research Overview
Fluid mechanics has been studied in the literature using both the Lagrangian and Hamiltonian formalism. In the classical Hamiltonian theory for fluid dynamical systems, a fundamental difficulty arises in incorporating the spatial boundary conditions of the system, which is also the case for general distributed parameter systems. Hamiltonian formulations of fluid flow in the literature tend to focus on conservative systems with no energy-exchange with its surrounding environment.
Usually, this is imposed by certain assumptions on the system variables. For example, if the spatial domain is non-compact, it is assumed that the system variables decay at infinity. Whereas if the spatial domain is compact, the boundary is assumed impermeable by imposing that the velocity vector field is tangent to the boundary.
Consequently, the traditional Hamiltonian theory is limited to distributed parameter systems on spatial manifolds without a boundary or ones with zero-energy exchange through the boundary. While this is useful for analyzing a system that is isolated from its surroundings, it is certainly an obstacle for practical applications such as simulation and control. While the traditional Hamiltonian formalism, in its generalized version on Poisson manifolds, focuses on conservative closed systems, the port-Hamiltonian formalism, based on Dirac structures, is applicable to non-conservative open systems capable of energy exchange with its environment.
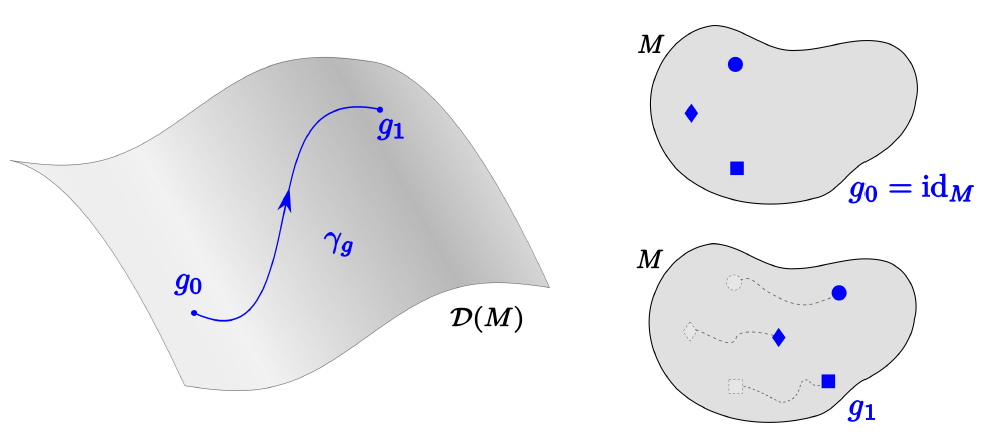
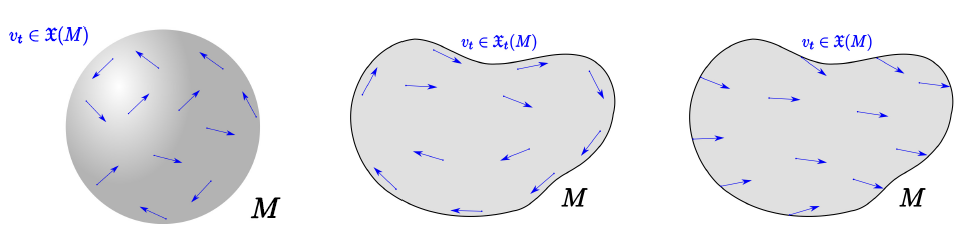
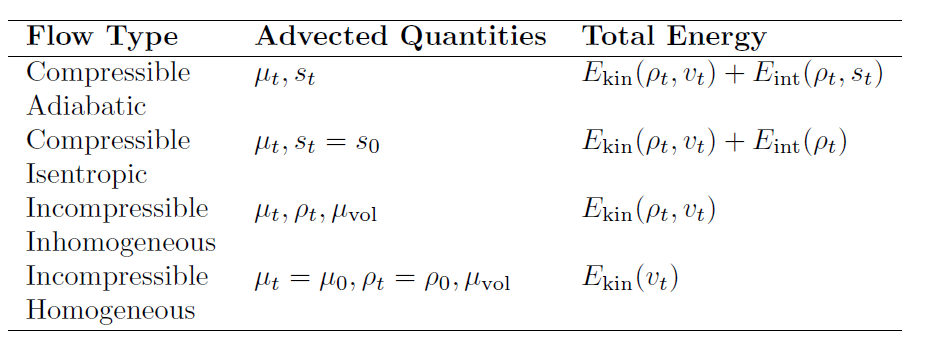
This work describes how fluid dynamical systems are systematically and completely modeled in the port-Hamiltonian framework by a small set of building blocks of open subsystems. Depending on the choice of subsystems one composes in an energetically consistent manner, the geometric description of a number of fluid dynamical systems can be achieved, ranging from incompressible to compressible flows. This decomposed network-based model of fluid dynamical systems comes at a great technical advantage. Each of the subsystems is described in the structurally simplest possible way, even if other subsystems require a considerably more sophisticated formulation. The composition of such unequal subsystems is mediated by a Dirac structure, which routes the energy flow between all subsystems.
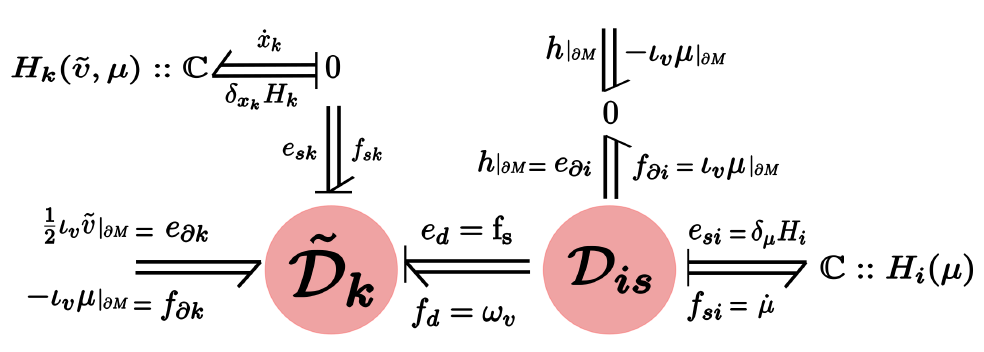
Publications
| Ramy Rashad, Federico Califano, Frederic P. Schuller, Stefano Stramigioli (2021) Port-Hamiltonian modeling of ideal fluid flow: Part I. Foundations and kinetic energy, Journal of Geometry and Physics 164, p. 104201, Elsevier B.V., doi:10.1016/j.geomphys.2021.104201 Ramy Rashad, Federico Califano, Frederic P. Schuller, Stefano Stramigioli (2021) Port-Hamiltonian modeling of ideal fluid flow: Part II. Compressible and incompressible flow, Journal of Geometry and Physics 164, p. 104199, Elsevier B.V., doi:10.1016/j.geomphys.2021.104199 |
